"Rigor Mates", parte IV: Los números reales.

Haciendo un recopilatorio de los capítulos de "Rigor Mates" (puedes verlos aquí: parte I, parte II, parte III), hemos ido ampliando sucesivamente el concepto de número ℕ⊂ℤ⊂, siguiendo un orden lógico, pero no histórico. Hoy nos ocuparemos de dar un paso más, ampliando  (el conjunto de los números racionales) mediante los números irracionales .

Como su propio nombre indica, los números irracionales son aquellos que no son racionales, es decir, que no pueden expresarse en forma de fracción. Ya en la antigua Grecia se sabía de su existencia, cosa que hacía que "se volvieran locos", y no es para menos. Intentad pensar por un momento como un discípulo de Pitágoras. Las Matemáticas que conoces están basadas en la geometría y la medida, y en ellas todo es perfecto e ideal. Pero aquí llega el triángulo rectángulo de catetos unidad y su hipotenusa de √2 unidades, que tienes "perfectamente" dibujada delante de ti, con su medida "exacta" (si quieres ver por qué pongo tanta comilla, deberías leer esta entrada), pero no puedes medirla, y nunca podrás (para saber más sobre este asunto, puedes leer esta otra entrada). He de decir aquí, que esta no era exactamente la situación, ya que el teorema de Pitágoras no se enunciaba como ahora lo conocemos, sino en términos de áreas, pero la reflexión que hemos hecho nos sirve para captar la idea.

Esquematización visual de las sucesivas ampliaciones del concepto de número.

Entonces, sólo nos falta la construcción formal y rigurosa (aunque al final aquí sólo demos la idea de esta construcción, que para nada es rigurosa XD), que esta vez es un poco diferente. En Matemáticas, hay un tipo de sucesiones llamadas de Cauchy que, grosso modo, son aquellas cuyos términos, a partir de uno dado, se aproximan cada vez más. Pues bien, llamaremos límite de una sucesión de Cauchy, si existe, a ese número al que se van acercando sus términos.

El quid de la cuestión está en que, para nuestro problema, consideramos sucesiones de Cauchy formadas por números racionales, cuyo límite podrá ser un número racional o no (y esto es lo importante), en cuyo caso será un número irracional. Y diréis, si si, todo ésto está muy bien pero, ¿cuál es la definición de conjunto de los números reales? Para ello, llamemos C al conjunto de las sucesiones de Cauchy de números racionales, y definamos en él la siguiente relación R (que resulta ser de equivalencia):

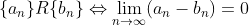La sucesión {a_n} y la sucesión {b_n}, están relacionadas si y sólo si la sucesión formada por la diferencia de sus términos tiene como límite 0.

Es decir, estamos relacionando dos sucesiones si ambas tienen el mismo límite. Como hemos mencionado, se demuestra que R es una relación de equivalencia y, por tanto, podemos considerar el conjunto cociente C/R. Pero, ¿qué conjunto es éste? Lo que hacemos al tomar cociente, es hacer indistinguibles aquellas sucesiones que tienen el mismo límite (que puede ser un número racional o irracional), identificando cada sucesión (o, mejor dicho, cada clase de sucesiones) con su límite, este conjunto no es más que el conocido conjunto de los números reales, y se denota como ℝ:=C/R. Como siempre, las propiedades y la estructura conocidas de los números reales, se deducen utilizando razonamientos rigurosos a partir de las de los números racionales y la construcción que hemos hecho.

El famoso número π es irracional. Otro día nos ocuparemos de los imaginarios.

Para terminar, hay que decir que, por supuesto, ésta no es la única manera de construir formalmente los números reales. Como ejemplo, podemos poner la construcción axiomática de Hilbert.

¡Síguenos en nuestra página de facebook!