Como ya hemos comentado, el orden que seguimos es un orden lógico y natural, pero no histórico. Aunque nos asombre al principio, si lo pensamos durante unos instantes, no parece tan sorprendente que "se descubrieran" antes los números racionales (positivos) que los números negativos (esto es, la ampliación de ℕ a ℤ) o, al menos, que éstos se aceptasen como números. Si no estáis de acuerdo conmigo, pensad qué os parece más aceptable, tener media manzana o tener -1 manzanas.
 |
| Recupero esta imagen que es muy socorrida XD |
Pero esto no es sólo cuestión de lo que a nosotros nos parezca, sino que los hechos así lo confirman. Aunque no se tiene constancia de que las antiguas civilizaciones egipcia y mesopotámica trabajasen con números negativos, sí que es más que sabido que conocían los números fraccionarios. En el papiro de Rhind se pueden encontrar fracciones de numerador 1, y es que los egipcios descomponían los números fraccionarios en sumas de fracciones de este tipo, siendo 2/3 la única que escribían sin descomponer.
Una vez hecho este repaso a la historia, vayamos al lío. Como dijimos en el anterior "Rigor Mates", los números enteros responden a la necesidad de restar, ya que los números naturales nos restringían a restas del tipo a-b con a>b (es decir, se podría restar 2-1=1, pero no 1-2). Algo parecido pasa con los racionales, que son la respuesta al problema de la división. Hasta ahora podemos dividir a/b sólo si a es múltiplo de b (por ejemplo, se puede dividir 2/1=2, pero no 1/2, y lo mismo con números negativos). Queda justificado, entonces, que es necesario hacer una ampliación de ℤ en la que la ecuación bx=a siempre tenga solución.
 |
| Los números racionales pueden tener infinitas cifras decimales, pero éstas son periódicas (repiten un patrón). Los irracionales, sin embargo, tienen infinitas cifras decimales no periódicas. |
Para ello, se procede de modo parecido a como lo hicimos en la ampliación de ℕ a ℤ. Consideremos, pues, el conjunto ℤxℤ cuyos elementos son las parejas (a,b), siendo a y b números enteros, y definamos en él la siguiente relación R:
De nuevo, análogamente al caso anterior, se demuestra que la relación R es de equivalencia y, por tanto, podemos considerar el conjunto cociente ℤxℤ/R, formado por las clases de equivalencia de las parejas (a,b) (la clase de equivalencia de (a,b) está por todos los (c,d) relacionados con él y, lógicamente, por él mismo). Y os preguntaréis, ¿qué narices está diciendo éste?, expliquémoslo.
Con la notación a la que estamos acostumbrados, una fracción es del tipo a/b (por ejemplo, 1/2, que se lee "un medio") donde a y b son números enteros, es decir, la pareja (a,b) de la que hablamos arriba en realidad sería la fracción a/b, y diréis, si, si, pero, ¿y lo de la relación? Pues, lo de la relación, es la manera de decir que dos fracciones equivalentes expresan el mismo número racional. Por ejemplo, las fracciones 1/2 y 2/4 expresan el mismo número, 0'5; con la notación de arriba, la primera sería el elemento (1,2) de ℤxℤ y la segunda, (2,4), que están relacionados, ya que 1*4=2*2 (si recordáis, éste es el método que nos enseñaron en el colegio para saber si dos fracciones son equivalentes).
Pues bien, denotando 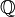 = ℤxℤ/R, queda perfecta y rigurosamente definido el conjunto de los números racionales
= ℤxℤ/R, queda perfecta y rigurosamente definido el conjunto de los números racionales 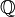 . A partir de la definición y utilizando las propiedades de los números enteros, se demuestran todas las de los racionales, entre ellas que la terna (
. A partir de la definición y utilizando las propiedades de los números enteros, se demuestran todas las de los racionales, entre ellas que la terna (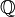 , +, *), donde + y * denotan a la suma y producto habitual de números racionales, es un cuerpo. Si recordáis, dijimos que (ℤ, +, *) es un anillo, esto es debido a que todos los elementos de
, +, *), donde + y * denotan a la suma y producto habitual de números racionales, es un cuerpo. Si recordáis, dijimos que (ℤ, +, *) es un anillo, esto es debido a que todos los elementos de 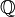 salvo el 0 tienen inverso para el producto * (el inverso de a/b es b/a), pero no los de ℤ.
salvo el 0 tienen inverso para el producto * (el inverso de a/b es b/a), pero no los de ℤ.
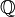 = ℤxℤ/R, queda perfecta y rigurosamente definido el conjunto de los números racionales
= ℤxℤ/R, queda perfecta y rigurosamente definido el conjunto de los números racionales 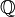 . A partir de la definición y utilizando las propiedades de los números enteros, se demuestran todas las de los racionales, entre ellas que la terna (
. A partir de la definición y utilizando las propiedades de los números enteros, se demuestran todas las de los racionales, entre ellas que la terna (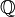 , +, *), donde + y * denotan a la suma y producto habitual de números racionales, es un cuerpo. Si recordáis, dijimos que (ℤ, +, *) es un anillo, esto es debido a que todos los elementos de
, +, *), donde + y * denotan a la suma y producto habitual de números racionales, es un cuerpo. Si recordáis, dijimos que (ℤ, +, *) es un anillo, esto es debido a que todos los elementos de 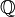 salvo el 0 tienen inverso para el producto * (el inverso de a/b es b/a), pero no los de ℤ.
salvo el 0 tienen inverso para el producto * (el inverso de a/b es b/a), pero no los de ℤ.
¡Síguenos en nuestra página de facebook!
No hay comentarios:
Publicar un comentario